2022-06-23 来源: 《银行家》2022年第1期
作者:吴永飞 等
2020年10月16日,习近平总书记强调,“要加强量子科技发展战略谋划和系统布局,把握大趋势,下好先手棋”。实际上,在众多新兴精尖技术中,量子计算由于其在机器学习建模应用方面表现出超越经典计算的模型准确性优势,在商业银行应用领域前景广阔。商业银行智慧运营场景为量子机器学习算法模型的应用提供了天然土壤,商业银行运营管理业务迎来了“换道超车”的发展机遇;将量子科技与银行智慧运营相结合,具有重要的社会价值和经济价值。当前社会已经从互联网、大数据时代迈向人工智能、量子科技时代,金融生态环境和客户交易习惯发生着深刻变化。在此背景下,银行需要以金融科技创新为驱动,全面推进运营管理数字化转型,在客户体验升级和资源配置优化等方面予以体现。本文将量子科技与机器学习相结合,立足我国商业银行应用实践,聚焦银行智慧运营场景,运用量子聚类技术为银行提供决策方案。
商业银行运营管理迎来智能化转型新机遇
银行物理网点作为银行服务客户的重要场所,其运营管理的效能优化对商业银行具有重要意义。如何在激烈的市场竞争中科学合理地配置资源,获得更长远的发展和更有效的竞争力,对每家银行而言尤为关键。虽然随着移动支付的普及,客户现金需求量减少,导致自动柜员机(ATM)的使用率下降,然而非现金业务离柜办理促进智能设备使用率上升,功能更多的机柜——智能柜台也在网点转型、融入新时代金融发展的背景下应运而生,越来越多的交易可在智能柜台上实现,它将银行零散琐碎的业务予以集中,原本需要大量人工的柜台业务成本得到了削减,效率也得到了提升,通过对硬件设备和业务流程的集成以及对交易凭证的整合,借助视频、影像、工作流、人脸识别等技术手段,智能柜台能将大部分的非现金业务都交由客户自助办理,这实现了业务迁移,缓释了柜面服务压力,进行客户分流,消解资源占用,延伸了智慧银行的发展方向。然而,在设备资源优化配置上,如何根据各网点的业务情况、运营情况来合理配置智柜设备数量,减少设备浪费和空闲情况,实现动态的设备数量配置管理,仍属于当前国内商业银行运营管理领域需要解决的问题。银行智能柜台设备管理的难点在于其分布范围广、数量多,所在地区客户和环境情况复杂等。为解决智能设备高效运营、精准布放的问题,可借助K-means聚类无监督学习方法,缩小对网点智柜设备业务的关注范围,直接聚焦到表现优异的网点集群和表现不理想的网点集群,有助于定期评估和掌握各网点智柜设备的运营管理情况,为进一步调整资源配置提供决策依据。
经典聚类与量子聚类算法模型
量子论诞生于20世纪初,作为现代物理学两大基石之一,改变了人们认识自然、解释自然的逻辑方法。但在量子论诞生的前大半个世纪,人们很少将其与计算、信息理论联系在一起,并没有看到量子论与其他学科进行交叉的巨大潜能。1986年,费曼(Feynman,1986)阐述了量子物理可对计算机算力的传统物理限制进行突破,一定程度上开启了量子计算的大门。量子计算与传统计算的最大不同主要是由于量子的叠加、纠缠以及相干等性质,对于经典算法有巨大的改进和提升。秀尔(Shor,1994)针对在经典计算机上难以求解的整数分解和离散对数问题,提出了大整数质因子分解的Shor算法。格罗弗(Grover,1996)提出了能够将在经典计算机上查询数据需要O(N)复杂度缩减至量子计算机上O()复杂度的量子搜索算法。
经典聚类分析
聚类分析是机器学习的主要任务之一。由于聚类是一种无监督的学习过程,即使是在没有先验知识标签的情况下也能够合理地按照数据自身的特征来进行样本归类,即“物以类聚,人以群分”。目前聚类算法大体上可以分为五类:一是划分方法,代表算法有K-means、K-medoids等;二是层次方法,代表算法有BIRCH、CURE等;三是密度方法,代表算法有DBSCAN、OPTICS等;四是网格方法,代表算法有STING、CLIQUE等;五是模型方法,代表算法有EM等。
K-means算法是划分聚类的典型代表之一,它具有算法简洁、运行速度快等优点;由于其无监督的属性,被广泛应用于在海量无标签数据集中寻找样本的相似性场景中。聚类不仅可以作为一个单独的过程来发现数据的内部分布结构,还可以作为有监督分类问题的预处理过程。例如,在一些商业应用中,可以先对没有标签的数据样本进行聚类,根据聚类结果进行样本标记,而后再利用有监督学习模型对分类样本进行训练和测试。
量子K-means算法
量子K-means算法是将量子特有的性质与传统K-means算法相结合,并对聚类精度有较大提升的一种量子机器学习算法。2012年,叶安新等人提出了一种量子粒子群算法的聚类方法,在一定程度上解决了聚类效果对初始质心敏感的问题;2013年,劳埃德(Lloyd)等人提出了量子版本的最近中心算法,该算法为量子K-means算法的子过程,主要是将量子态的内积转化到一个量子态的振幅上,进而可以计算出量子态之间的相似度;2015年,潘建伟团队在小型光量子计算机上首次实现了Lloyd提出的量子K-means算法;2017年,刘雪娟等人通过量子并行方案和量子搜索算法来提高K-means算法的效率,并证明了在一定条件下,量子K-means算法在时间和空间复杂度方面都存在明显优势;2021年,李玥等人利用量子粒子群优化算法的全局搜索能力强、收敛速度快等优势,提出了改进量子粒子群的K-means聚类算法,该改进算法在精度、速度和稳定性上都有显著提升,同时也在一定程度上解决了聚类效果对初始质心敏感的问题。
量子聚类算法模型在银行智慧运营场景的应用
本文运用量子K-means聚类算法,对商业银行支行网点的智能柜台运营情况进行聚类分析。聚类分析的过程:首先根据智能设备的各类描述性特征指标情况,对设备所属支行网点开展数据样本的无监督聚类;再根据聚类结果中每一类的类核质心特征开展对该类别的业务描述和定义,这里需要人为对各类别进行标签化定义,如“设备繁忙且人工维护及时的优异支行”“设备繁忙但人工维护差的需加强人工维护支行”“设备空闲而人工维护情况好的需减少设备支行”等。根据类别标签定义,最终寻找出在智能设备管理中表现优秀的机构群体和待优化的机构群体。
数据来源与特征工程
本文选取国内某股份制商业银行744家支行网点的智能设备运营数据作为样本,范围覆盖全国31个省、直辖市、自治区,数据来源为智能设备监控报表数据和流水日志,数据时间范围跨度为两年,其中使用不足两年的设备,按其实际使用时间内的数据进行建模。为构建量子K-means算法模型,本文选定特征参数,通过取均值、中位数、方差等统计学方法对报表数据进行计算加工,最终降维至两个特征参数,分别为代表设备维护情况的维护指标和代表设备业务量情况的业务指标。
构建量子K-means算法模型
本文的量子K-means算法模型是在量子最近中心算法的基础上构建的,主要是通过将样本特征和聚类中心的特征压缩到两个量子态|Φ>和|ψ>中,运用Controlled-SWAP门和Hadamard门将两个量子态的距离转移到第一个控制比特上,可以通过计算得到:
其中为两个量子态之间的距离,其线路图如图1所示。
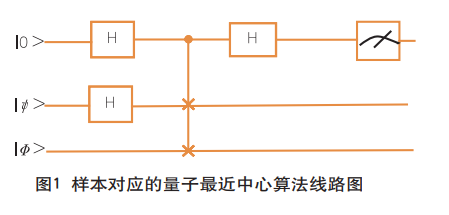
通过上述量子最近中心算法可以对传统K-means算法进行量子化改进,设计出如下的量子K-means算法:
输入:样本集D={x1,x2,…,xm},聚类个数K,量子K-means线路,迭代次数m。
过程:
1.从D中随机选择K个样本作为初始质心{μ1,μ2,…,μk}
2.repeat m
3. 令Ci=Φ(i=1,2,…,k)
4. for j=1,2,…,m do
5. 将xj和聚类中心的特征压缩后作为参数嵌入至量子K-means算法的U门;
6. 根据量子最近中心算法得到距离样本j最近的质心,假设为μT;
7. 将xj划入对应的类CT;
8. end for
9. for i=1,2,…,K do
10. 计算新的均值向量
11.end for
输出:聚类C={C1,C2,…,Ck}
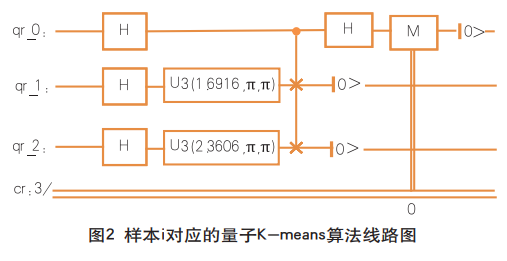
图2展示了某个样本i完整的量子K-means算法的线路图。
量子K-means算法模型结果
基于IBM Quantum Experience量子计算实验环境,量子K-means算法模型将744家支行网点聚为三类,根据质心结果可以得出,第0类支行为智能柜台业务量大且设备维护情况良好的优异支行,第1类支行为智能柜台业务量大但是维护情况欠佳的支行,第2类支行为智能柜台业务量小而维护情况良好的支行。根据这三类支行情况,建议分别采取措施对网点智能设备进行优化,对于第1类支行可以加强人工维护频率和及时性,而对于第2类支行可以进行设备裁撤。为说明量子K-means算法的有效性,将基于智能设备运营数据得到的量子K-means模型结果和经典K-means模型结果进行对比,如图3所示。
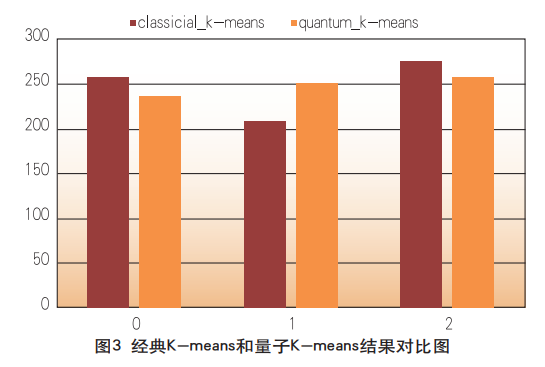
从图3可以看出,量子K-means结果为236家支行属于第0类,251家支行为第1类,257家支行为第2类。表明量子K-means模型和经典K-means模型的聚类结果基本一致。为了验证量子K-means模型的聚类结果有效性,图4给出了量子K-means模型和经典K-means模型聚类结果的混淆矩阵。
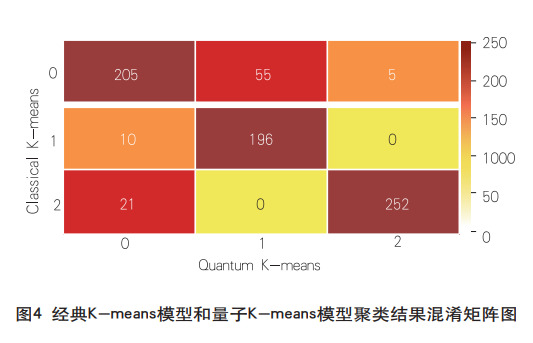
从图4可以看出,对于88%的样本而言,量子K-means模型和经典K-means模型的聚类结果完全一致,这进一步说明使用量子线路转化得到的量子态内积作为“距离”和经典的欧几里得距离是等价的;同时,我们对剩余12%的聚类不一致样本(91个)进行了专家经验判断,其中经典K-means模型与专家经验有5/91的样本保持一致,而量子K-means模型与专家经验有68/91的样本保持一致,因此以专家经验为参照来看,量子K-means模型的准确性更高,同时这也展现了量子K-means算法模型的有效性,由此实证了量子K-means算法在无监督学习方面的优越性。
结语
本文针对银行运营管理中的智能柜台布局优化场景,运用前沿的量子K-means算法模型,给出聚类分析结果和资源配置优化建议方案,为商业银行运营管理数字化转型提供了科学的决策依据,符合数字经济时代商业银行数字化转型的整体战略要求。未来我们将进一步聚焦以量子技术优化传统智能算法领域,并将算法深入应用在商业银行风险管理、营销管理等方面,扩大量子机器学习算法模型在银行和金融领域的应用价值。
(本文合作作者有王涛、王彦博、张立伟、关杏元、项金根、史杰、徐奇、杨璇和高新凯,其中王彦博〔wangyanbo@lyzdfintech.com〕为本文通讯作者。)
(作者单位:华夏银行股份有限公司,龙盈智达〔北京〕科技有限公司)
责任编辑:魏敏倩