光子隐私计算在金融领域的应用研究

作者：吴永飞 金贤敏 王彦博 李大伟

 

数字经济时代，数据作为新型生产要素为生产力带来了全新的变革，在充分盘活数据价值的同时，做好数据安全保护工作已成为重中之重。2021年9月1日，《中华人民共和国数据安全法》正式施行，数据安全已上升至国家法律高度。金融行业作为数据密集型行业，一直以来都将数据安全视为“生命线”，并不断采取多种技术保障数据安全。本文立足商业银行视角，基于光子金融科技框架，创新将光子密码学引入金融科技，以期为商业银行提供受物理学定律保护的光子密码学技术应用新思路，为金融机构在数据安全合规的前提下充分释放数据要素潜能提供新方案。

 

隐私计算概述

 

隐私计算（Privacy Computing）是在保护数据本身不对外泄露的前提下实现数据分析计算的技术集合，一般而言主要包含多方安全计算、联邦学习、可信执行环境等技术方向。

 

多方安全计算于1982年由姚期智^[1]首次提出，可以保证在不透露各参与方数据信息的前提下完成多方共同计算的任务。当前，多方安全计算领域常用的技术包括秘密共享、同态加密和零知识证明等。目前已经有诸多机构和专家学者开展了对多方安全计算的相关研究与应用。2020年11月24日，中国人民银行发布《多方安全计算金融应用技术规范》（JR/T 0196-2020），对多方安全计算技术在金融领域的应用制定了相应要求。同年，谭培强^[2]等人将多方安全计算技术应用于金融数据治理，在保证数据安全的情况下深挖数据价值。2021年，光大银行上线企业级多方安全计算平台，可应用于联合营销、联合风控、业务合规等多个领域^[3]。2022年，交通银行搭建了多方安全计算技术平台，并应用于商业银行风控、营销等场景^[4]。

 

联邦学习于2016年由McMahan等人首次提出，属于一种机器学习框架，可分为加密样本对齐、加密模型训练与效果激励三部分。2020年，阳文斯^[5]基于联邦学习提出了一种带隐私保护的信用卡欺诈检测方法和系统，能够保证银行在不上传私有数据集的情况下完成建模任务，从而保障银行用户的数据安全。2022年，关杏元^[6]等人研究了隐私立法时代联邦学习在商业银行的应用，基于联邦学习的隐私计算平台能够解决数据合规问题，打破数据壁垒，拓宽金融数据使用的边界。同年，常悦^[7]等人提出了基于联邦学习的风控模型，该模型能够让多个机构实现数据共享，解决了因信息不对称带来的融资难问题。2023年，陈彤^[8]等人在华夏银行北京分行从助贷业务反欺诈场景入手，为降低行内互联网渠道消费贷产品的欺诈风险，提高自主风控能力，在获得客户授权的情况下，使用联邦学习计算技术构建贷前反欺诈模型，取得良好的模型效果。同年，刘紫微^[9]等人基于ResNet深度神经网络模型与联邦学习进行融合建模，提出一种新的信用风险预测方法，首次采用“联邦优化算法—局部全局联合平均算法”优化训练过程，对贷款用户构建信用风险识别模型，实现信用风险预测并保证用户数据的隐私安全。

 

无论是多方安全计算还是联邦学习都离不开对数据的加密，同态加密是一种在密文上做运算和明文做运算保持一致的加密算法。同态加密从计算类型与支持计算的程度视角来看，可分为半同态加密、部分同态加密和全同态加密。作为一种特殊的加密机制，同态加密在1978年被Rivest^[10]等人首次提出，他们利用RSA公钥加密体制以及求幂函数实现了乘法同态加密和加法同态加密，但此方案的安全性无法保证。2009年，Gentry^[11]构造出一个全同态加密方案，是密码学研究中的一次重大突破。2017年，Cheon等人^[12]提出CKKS全同态加密算法，支持针对实数或者复数的浮点数加法和乘法同态运算，得到的计算结果为近似值，在隐私保护和云计算等领域有广泛的应用。2020年，王婧琳^[13]提出了基于同态加密的金融数据安全共享方案，从金融领域的视角出发，对金融数据安全共享方案的结构、流程和算法这三方面进行详细设计。2022年，袁露^[14]基于多元线性回归和同态加密技术，设计了纵向联邦学习的训练和预测模型，在训练阶段去除第三方，避免数据暴露，也直接杜绝了合谋攻击，同时使用Paillier同态加密算法来加密梯度信息，避免参与方的原始特征值和特征参数直接参与模型训练，提高了数据和模型的安全性及隐私性。

 

光子密码学助力隐私计算发展

 

近年来，光子金融科技蓬勃发展。作为光子金融科技的重要领域之一，光子密码学与隐私计算的结合在金融领域也展现出广阔的应用前景。

 

1995年，Refregier和Javidi^[15]提出了具有开创性的光学加密方案，即基于傅里叶变换的双随机相位加密方法。在该加密方案中，利用两个随机相位板分别放置在4F系统（一种光学成像系统，可以利用光学傅里叶变换技术、光学相干技术进行二维处理，实现图像加减、图像微分等）的输入面和频谱面中，可以实现对原图像信息分别在空域上和频域上的调制，使得原图像在输出面变成一幅看不到任何轮廓的无规则图像，实现对原图像信息的加密。目前已有诸多光学加密技术，如利用离轴数字全息的加密方法、基于分数傅里叶变换的加密方法和基于相位恢复算法的加密方法等。2020年，许祥馨^[16]等人提出了一种基于双随机相位编码的局部混合光学加密系统，该系统能够实现对图像中的部分信息进行加密。2022年，英国Optalysys公司提出了一种基于光子计算的全同态加密技术方案，在该方案中信息可被编码成许多不同光束的相位和振幅。这些信号会被称为波导的结构引导到特定的方向，然后将其照射到自由空间中，在此空间中信号会合并和相互干涉，从而能够直接在加密数据上进行计算，以此可以提升全同态加密的运算效率。

 

综上可知，光子密码学与隐私计算天然具有融合的可能，积极探索基于光子特性的隐私计算效率提升新方案具有重要价值。

 

光子隐私计算在联合风控中的应用探析

 

业务理解与数据理解

 

金融机构在给客户授信时，不仅需要考虑贷款人在本行的贷款情况，往往还需考虑贷款人在其他金融机构的贷款情况，从而避免重复过度授信。鉴于各金融机构的客户贷款信息均属保密信息，此时需要设计一套算法机制，实现在不透露隐私的情况下得到贷款人在各金融机构的贷款总额。

 

具体来看，假设客户C要向金融机构B贷款，金融机构B还需要了解其他金融机构针对客户C的授信总额r，但不需要知道客户C在其他各家金融机构的具体授信金额。同态加密能够有效地解决这一难题，即可以使用加法同态加密技术对客户C在其他金融机构的贷款情况进行加密，若C在第k家机构的授信金额为l^k，则加密后的金额为：

 

y_k=m(l^k)

 

其中m表示加法同态加密技术的加密过程，y_k是加密后的结果，加密技术可以使用Paillier或Cheon-Kim-Kim-Song（CKKS）等同态加密技术对l^k数据进行加密。由于加法同态可实现在密文上做某些运算等价于在明文上做加法运算，此时可以通过同态加密运算给出客户C在各金融机构的授信总额r，确定该客户是否存在过度授信的风险。

 

针对上述场景进行抽象，假设贷款客户C在两家金融机构有授信，每家金融机构对客户C的授信金额分别为1.123千万元和6.914千万元（上述金额不为第三家金融机构所知）。由于在整个隐私计算过程中会涉及到大量的高阶多项式乘法运算，使用经典计算机进行运算极其耗时。因此，本研究基于全同态加密CKKS方案，发挥CKKS作为近似精度计算方案的优势，并进一步运用光学高并行性的特性进行加速，为基于同态加密的隐私计算提供光子化解决方案。

 

模型构建

 

本研究采用全同态加密技术CKKS对授信数据进行加密，整体方案如下：首先通过数据编码将待计算数据编码到多项式的系数中，然后使用CKKS方案中生成的公钥对数据进行加密，而后在密文上进行多项式运算，再针对密文计算的结果进行解密，最终得到待计算明文的和。具体流程如下。

 

编码过程

 

将明文数据a₁和a₂编码到多项式环上，其系数向量记分别为m₁和m₂。本研究使用的多项式环Z_q[X]/(Xⁿ+1)中n为1024，取模的数q选取134215681（转化为二进制数是27位）。

 

密钥生成过程

 

随机生成一组随机数（s，a，e），每个随机数表示一个1024阶多项式环的系数向量，其中s中每个数的取值范围为{0,1,-1}，e中每个数的取值为[0,134215680]的随机分布，e中每个数的取值服从高斯分布，而后根据加密方案可以计算出b：

 

b= -as+e

 

上式中as表示多项式环上的乘法运算，整个计算过程包含hadamard积运算和取模运算，运算过程等价于进行negative-wrapped卷积运算。通过计算后即可得到公钥p_k=(b,a)，私钥为(1,s)。

 

 加密过程

 

利用公钥p_k对编码的多项式系数m₁和m₂进行加密，公式如下：

 

C₁=(C₁₀,C₁₁)=u₁p_k+(m₁+e₁₀,e₁₁)

C₂=(C₂₀,C₂₁)=u₂p_k+(m₂+e₂₀,e₂₁)

 

其中u₁、u₂、e₁₀、e₁₁、e₂₀、e₂₁分别为随机生成的数值，其中u₁和u₂表示一个1024阶多项式的系数向量，每个数的取值范围为{0,1,-1}，e₁₀、e₁₁、e₂₀、e₂₁中的每个数值为[0,134215680]的随机分布。将密文C₁和C₂求和可得：

 

C₃=(C₃₀,C₃₁ )=(C₁₀+C₂₀,C₁₁+C₂₁ )

 

解密过程

 

利用私钥，根据公式对C₃进行解密得到明文P，计算如下：

 

P=C₃₀+C₃₁s

 

对明文P进行多项式采样并缩放后得到计算结果r。

 

光子计算加速原理

 

光计算以其内在的并行性、超高的带宽优势、极低功耗和强大的可重构能力，为下一代高性能计算提供了天然的支撑。此外，伴随着硅基光电子技术的飞速发展，集成光计算已经逐渐成为突破电计算芯片性能极限和续写摩尔定律的技术选择。

 

从硬件实现来看，本研究使用的光子芯片由光学硅的薄膜铌酸锂（LNOI）材料制作，其具有高调制速率、高带宽、低损耗等特点，调制速率可以达到数十GHz量级，与传统的数十KHz热光调制相比，同等规模的网络可以实现几个数量级的性能提升。以薄膜铌酸锂制作的光芯片，可以工作在几G甚至几十G工作频率上，可以极大地提升芯片算力。

 

从算法方案来看，研究方案中CKKS加密算法中的公钥生成、加密部分和解密部分均涉及到多项式环上的乘法运算，在运算中涉及到向量之间的hadamard积运算，可以利用光子计算高并行性的优点，采用光子芯片对hadamard积运算进行加速，进而加速CKKS加密算法。具体而言，基于光子芯片加速hadamard积运算的示意图如图1所示。

 

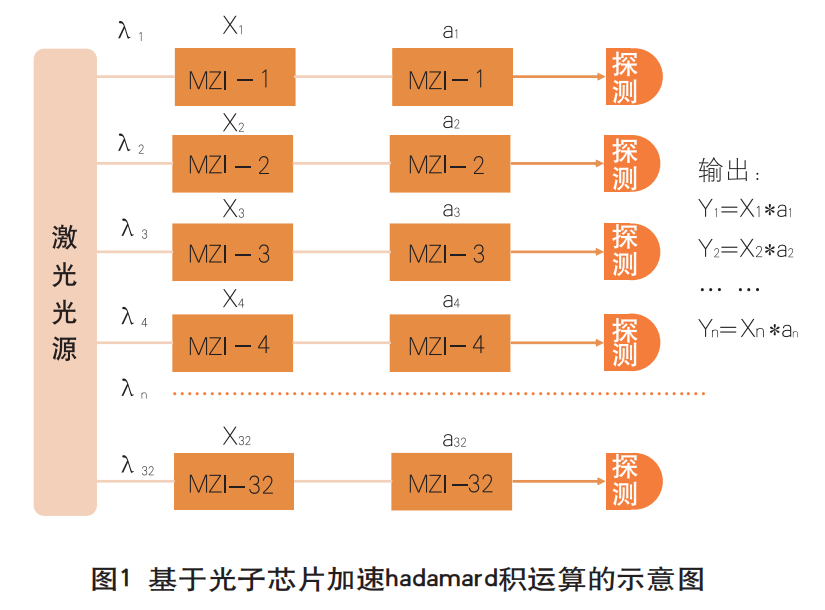
图1是基于高速可调LNOI芯片的32维向量光学点积计算系统，该系统可以实现hadamard积运算加速作用：如实现两个向量x=(x₁,x₂…,x_n)和向量a=(a₁,a₂…,a_n)的hadamard积运算，首先系统采用多个波长的光分别通过高速MZI调制器，通过改变MZI两臂相位差实现光的强度调制，使得数据使用振幅编码的方式加载到光信号中，随后经过强度调制的各个波长的光通过合束器进入光电探测器被检测，光电探测器的输出即为向量hadamard积结果。目前由于受到系统工程化规模限制，尚无法一次性完成维度为1024的大规模向量的hadamard积计算，因此本文通过将大维度向量hadamard积计算拆分为细粒度的hadamard积操作进行计算予以实现。

 

实证分析

 

从算法实现来看，通过上述过程对a₁=1.123，a₂=6.914进行编码、加密、运算和解密采样得到最终的结果，整个过程使用光子芯片进行加速，计算的结果r约为8.03，而在明文上两个数值的真实和为8.037，二者（密文近似计算结果与明文计算结果）误差仅为0.087%，初步验证了基于CKKS算法实现光子同态加密方案的有效性。具体到联合风控业务场景，即金融机构B可知客户C在其他多家金融机构的授信总额约为8.03千万元，该汇总数据信息有助于业务端对客户是否过度授信进行直观判断。

 

从加速效果来看，光芯片加速时间主要体现在加速hadamard积运计算过程上，以主频是1GHz、单核、单指令测算，传统电子芯片计算一个1024维向量的hadamard积运算需要约1024纳秒，而使用光子芯片（采用32维的hadamard积运算最小计算核，执行32维向量的hadamard积运算需要时间约为1纳秒）则需要约为32纳秒，较传统方法计算效率提升约为32倍；对于整个1024阶多项式环上乘法运算，使用传统电子芯片计算完成一次计算的时间约为13微秒，由于对于其中的hadamard积运算进行了光子加速，所以加速后完成一次计算的时间约为7微秒，较传统方法计算效率提升约为2倍，进一步验证了光芯片的加速效果。

 

结语

 

数字经济时代，光子金融科技作为光子科技和金融科技相结合的交叉领域方兴未艾。本文面向商业银行业务场景，创新将光子密码学引入到隐私计算中，运用光子科技特有的性质，初步验证了光子同态加密技术在商业银行隐私计算场景应用的可行性，在有效提升同态加密计算效率的同时还保证了数据信息的安全，为商业银行隐私计算的发展和创新提出了光子化解决方案。

 

【参考文献】

[1] Yao A C . Protocols for secure computations[C]. Proc. of the 23rd Annual IEEE Symposium on Foundations of Computer Science, 1982:160-164.

[2]谭培强,谢谨.多方安全计算助力金融数据治理[J].中国金融,2020(22):39-40.

[3]刘巍,曹伟.多方安全计算助力光大数字化生态协同[J].金融电子化,2021(12):52-53.

[4]李肇宁,钱菲,王光中.利用多方安全计算技术构建数据融合新利器[J].金融电子化,2022(2):63-65.

[5]阳文斯. 基于联邦学习的信用卡欺诈检测系统研究[D].中国科学院大学(中国科学院深圳先进技术研究院),2020.

[6]关杏元,王彦博,李晓林,张月. 隐私立法时代联邦学习在商业银行的应用[J]. 银行家,2021(12):116-119.

[7]常悦. 基于联邦学习的大数据风控模型[D].郑州大学,2021.

[8]陈彤,汪秀山,王湾湾,王丽波. 隐私计算赋能银行助贷款业务自主防控[J/OL]. 金融电子化, 2023.

[9]刘紫微,郑山红. 基于一种新的联邦优化算法的信用风险预测方法[J]. 长春工业大学学报,2023,44(01):58-64.

[10]Rivest R L, Adieman L, Dertouzus M L. On Data Banks and Privacy Homomorphisms [J]. Foundations of Secure Computation，1978，4(11):169-179.

[11] Gentry C. Fully Homomorphic Encryption Using Ideal Lattices[C]. Annual ACM symposium on Theory of computing, 2009:169-178.

[12] Cheon J H, Kim A, Kim M, et al. Homomorphic Encryption for Arithmetic of Approximate Numbers[C]. International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 409-437.

[13]王婧琳. 基于同态加密的金融数据安全共享方案研究及实现[D].哈尔滨工业大学,2020.

[14]袁露. 基于同态加密的纵向联邦学习关键技术研究[D].华东师范大学,2022.

[15] Refregier P, Javidi B . Optical Image Encryption Based on Input Plane and Fourier Plane Random Encoding[C]. Optical Implementation of Information Processing. International Society for Optics and Photonics, 1995.

[16]许祥馨,常军,武楚晗,宋大林. 基于双随机相位编码的局部混合光学加密系统[J]. 物理学报, 2020, 69(20):229-239.

 

(华夏银行信息科技部陈志豪，上海图灵智算量子科技有限公司王瑞、彭于权，以及龙盈智达﹝北京﹞科技有限公司杨璇、徐奇、曹晓峰、冯琳、王杰对本文亦有贡献。)

 

（作者单位：华夏银行股份有限公司，龙盈智达﹝北京﹞科技有限公司，上海图灵智算量子科技有限公司）

 

责任编辑：张志敏