数字金融 | 数字时代风控新范式——量子安全隐私计算

作者：涂 锟  黄安静  张凯羿  郁 昱

原标题：量子安全隐私计算技术体系研究和应用探索

 

数字化浪潮下，金融行业作为经济核心正处于转型期，同时面临双重挑战。一方面，数据孤岛与隐私壁垒阻碍了跨机构协同合作，导致效率低下。从反欺诈角度看，全球诈骗案件数量从2020年的2.66亿起攀升至2021年的2.93亿起，增长10.2%；损失金额从478亿美元增长至553亿美元，增幅达15.7%。我国电信网络诈骗形势严峻，2020年涉及财产损失达353.7亿元^[1]。在反洗钱领域，2024年区块链安全事件频发，共410起，损失金额达20.13亿美元^[2]。这些数据表明，金融行业在反欺诈与反洗钱方面遭受巨大经济损失。另一方面，量子计算领域突破性进展正在动摇传统密码学根基。据权威研究预测，到2026年，主流公钥加密体系被量子攻击破解概率达14%，到2031年风险攀升至50%。在此严峻形势下，构建覆盖数据全生命周期的量子安全防御体系，成为金融行业生存与发展的关键^[3]。

 

量子信息技术与金融安全深度融合，为数字经济时代风险防控带来全新范式。通过量子密钥分发（QKD）、量子不经意传输（QOT）与后量子密码（PQC）三者协同创新，构建全方位安全体系，从底层通信到上层应用为金融行业提供坚实防护。

 

面向金融业务的量子安全隐私计算技术架构

 

金融业务的隐私计算需求呈现出多层次、多模态的特点，涵盖了从基础线性运算到复杂非线性模型的整个计算链条。然而，传统的隐私计算方案在应对金融场景时，暴露出两大核心矛盾。对于线性函数计算，如数据聚合、统计计算等，需要高效的同态加密技术支持。但经典同态算法不仅面临着无法抵御量子攻击的风险，而且计算开销过大，这成为了制约其应用的瓶颈。在非线性函数计算方面，像风险评估、关联分析等复杂金融模型都依赖多方安全计算协议，然而传统的不经意传输（OT）协议在量子攻击下，安全性会出现坍塌。为有效应对上述挑战，研究人员创新性地提出了一套解决方案：如图1所示，通过分层融合量子密钥分发（QKD）、量子不经意传输（QOT）与后量子密码（PQC）技术，构建起一个全面且高效的隐私保护体系。该体系具有显著优势，是能够覆盖从基础线性运算到复杂非线性模型的全计算范式，能够为各类计算场景提供可靠的隐私保障。

 

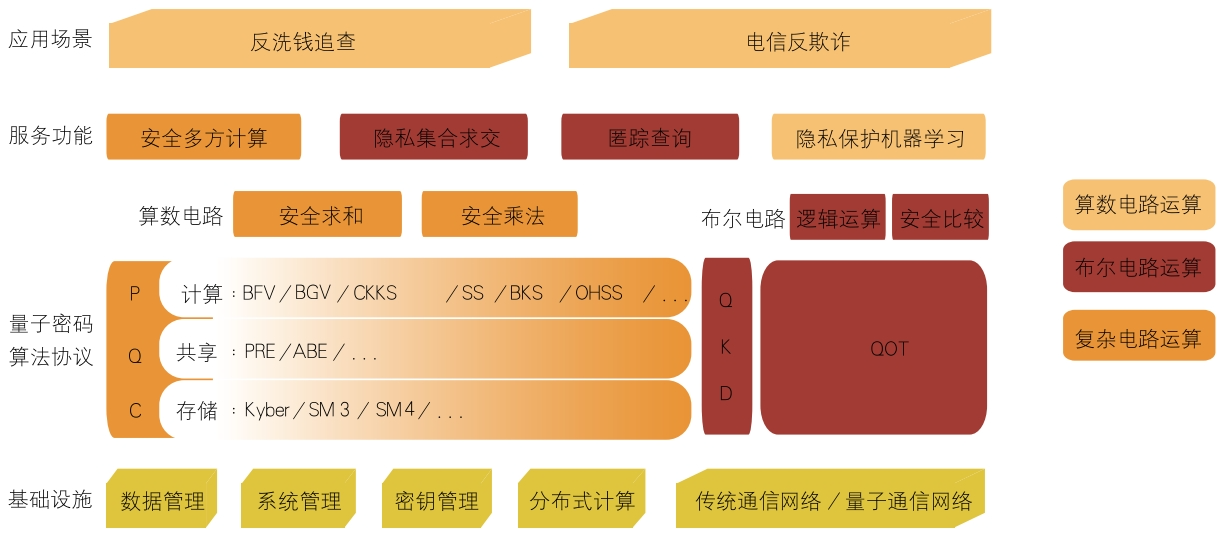
图1 后量子密码与量子密钥分发共同构建后量子隐私计算体系

 

在处理线性函数的高效加密计算时，传统安全两方计算协议通常涉及加法和乘法运算。其中，加法运算在多数方案中可以较为轻松地实现线性处理，而乘法运算则一直是安全多方计算中的核心难题。目前的解决方案主要包括秘密共享和同态加密技术，这两种方法各有优劣：秘密共享方案计算开销较低，但通信成本较高；而同态加密方案则相反，通信开销低，但计算需求大。

 

为了在量子安全的框架下平衡两者的优缺点，同态秘密共享（HSS）这种混合方法应运而生。它整合了秘密共享和同态加密的优势，在安全多方计算环境中实现了计算和通信复杂性之间的平衡。然而，现有的HSS技术主要适用于通用的安全多方计算场景，对于复杂计算场景，如安全两方矩阵-向量乘法和矩阵-矩阵乘法，还无法提供有效的支持。鉴于这些计算在隐私保护机器学习领域的重要性，扩展HSS技术以适应这些复杂场景显得尤为关键。

 

S Zhang等（2024）^[4]创新性地提出了基于HSS的“矩阵-向量乘法”和“矩阵-矩阵乘法”方案，进一步证明了这一研究方向的重要性和可行性。《金融反欺据存储、数据共享和数据计算构成了数据价值流转的核诈与大数据风控研究报告（2023）》[2]的设计思路如图2所示。

 

               

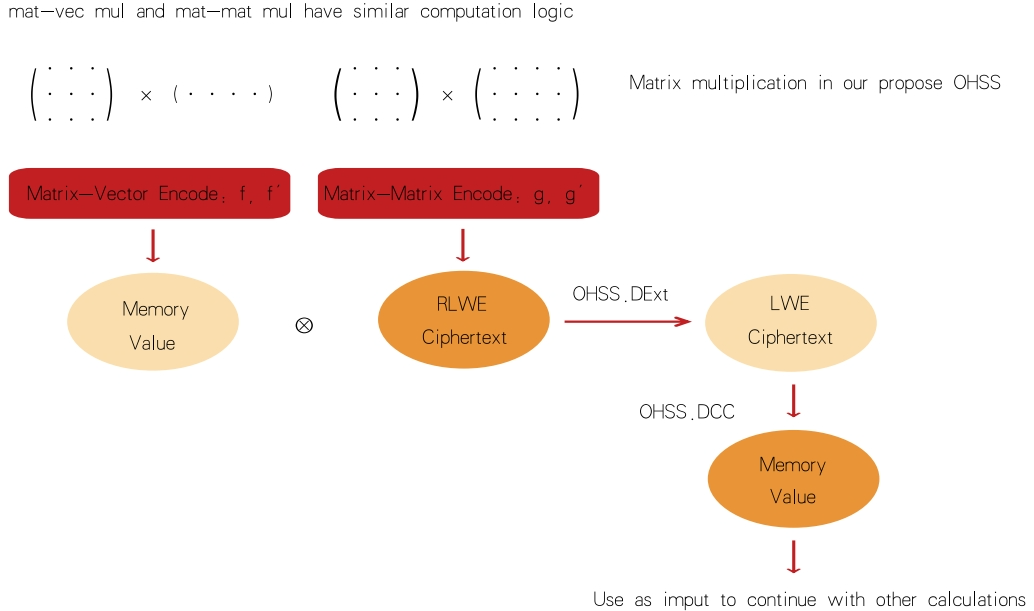
图2 基于OHSS的矩阵向量乘法

 

在实现非线性函数的安全多方协作方面，复杂金融模型，如信用评分模型、反洗钱关联图谱等，都依赖于非线性函数的隐私计算。以跨机构黑名单比对场景中所需要的隐私集合求交为例，如图3所示，通过特定的量子不经意传输（QOT）协议，利用偏振编码量子态与哈希承诺机制，重新构建了多方安全计算的基础算子，进一步支撑双方在不泄露输入集的情况下完成交集运算。其安全性仅依赖抗碰撞哈希函数假设，相比经典OT协议所依赖的离散对数假设更为弱化。再结合量子密钥分发网络提供的动态密钥，这一方案能够抵御量子存储攻击，满足金融数据安全分级指南中的最高隐私保护等级^[5]。

 

                   

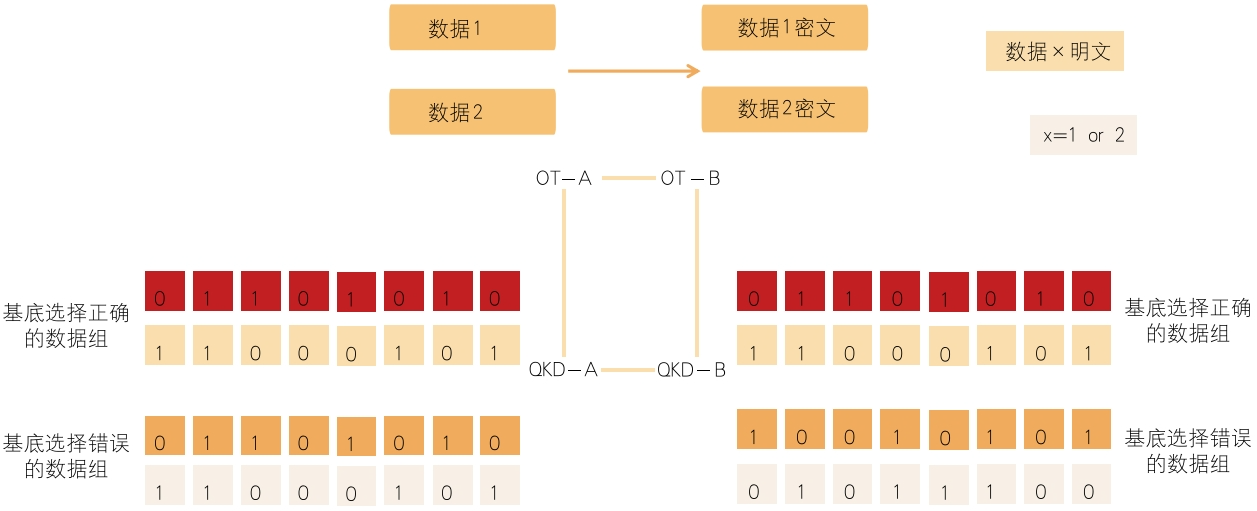
图3 QOT协议流程示意图

核心协议创新：从理论突破到工程落地

 

在隐私计算体系中，将后量子高阶密码学原语，如基于格的同态加密、秘密共享和同态秘密共享等，与已有的抗量子不经意传输（OT）相结合，能够显著拓展功能边界、优化计算效率并增强安全性。这种结合不仅可以实现两方隐私计算，还能实现多方隐私计算。

 

后量子密码保障数据生命周期安全

在数字化进程不断加速的当下，数据流通成为释放数据价值的关键驱动力。在这个数据流通的时代，数据存储、数据共享和数据计算构成了数据价值流转的核心环节，而针对这些环节设计行之有效的后量子密码保护方案至关重要。

 

在数据存储领域，Kyber^[6]、SM3^[7]、SM4^[8]等方案被广泛采用。其中，基于格的加法同态加密算法发挥着关键作用。该算法依托格密码学独特的数学结构，生成能够抵御量子计算机破解的密钥。借助这一密钥，在不泄露数据隐私的前提下，可对加密数据进行加法运算，为数据存储筑牢安全防线。与此同时，秘密共享技术（SS）的引入进一步强化了数据的隐私保护机制。它将数据分割存储于不同参与方，只有在满足一定数量参与方共同协作时，才能还原出原始数据。这种加法同态加密与秘密共享相结合的存储方案，不仅显著提升了数据的安全性，还为后续的数据计算工作提供了极大的便利。

 

在数据共享环节，基于格的代理重加密^[9]、属性加密^[10]等先进技术发挥着重要作用。这些技术在充分保障数据隐私的基础上，实现了数据在不同参与方之间的合理共享。通过精准的权限控制和加密处理，有效平衡了数据的可用性与安全性，确保数据在流通共享过程中的价值得以充分释放，同时又不危及数据所有者的隐私权益。

 

在数据计算方面，创新性地融合了基于格的加法同态加密、全同态加密、秘密共享和同态秘密共享四种算法。基于格的加法同态加密算法能够支持简单的数据处理任务，为基础计算提供安全保障；全同态加密技术则突破了传统加密的限制，可对加密数据进行复杂的算术计算，涵盖加法和乘法运算，真正实现了数据“可用不可见”的安全计算模式；秘密共享和同态秘密共享技术通过将数据分割计算，在提升数据安全性的同时，还大幅提高了计算效率。这一综合性计算方案具备强大的功能，能够支持各类复杂计算任务，确保在整个计算过程中数据隐私和安全万无一失。

 

QOT在性能和安全性两方面的突破

基于QKD的BB84协议，创新性地构造了量子不经意传输（QOT）协议。该协议具备多方面的优势。从抗量子攻击特性来看，密码技术是隐私计算安全的基石。融合量子信息技术的密码学假设结构中，不同的假设强度不同，相应的密码算法或协议可靠性也有所差异。经典的OT协议通常基于公钥密码实现，依赖传统密码学假设，在量子计算时代存在明显的安全隐患，容易受到量子攻击。而QOT协议，通过使用QKD和对称密钥加密构建。如图4所示，它所基于的密码学假设比经典OT更弱，甚至比后量子密码构建的OT协议（PQC-OT）还要弱。这是因为该协议仅需要量子安全的比特承诺方案，此方案依赖于单向置换或抗碰撞性哈希函数，这两者都属于无结构的对称数学问题，量子计算机难以破解，并且单向函数是量子领域中所需的最小假设。因此，从理论分析上，QOT协议具备更强的抗量子安全性。

 

                

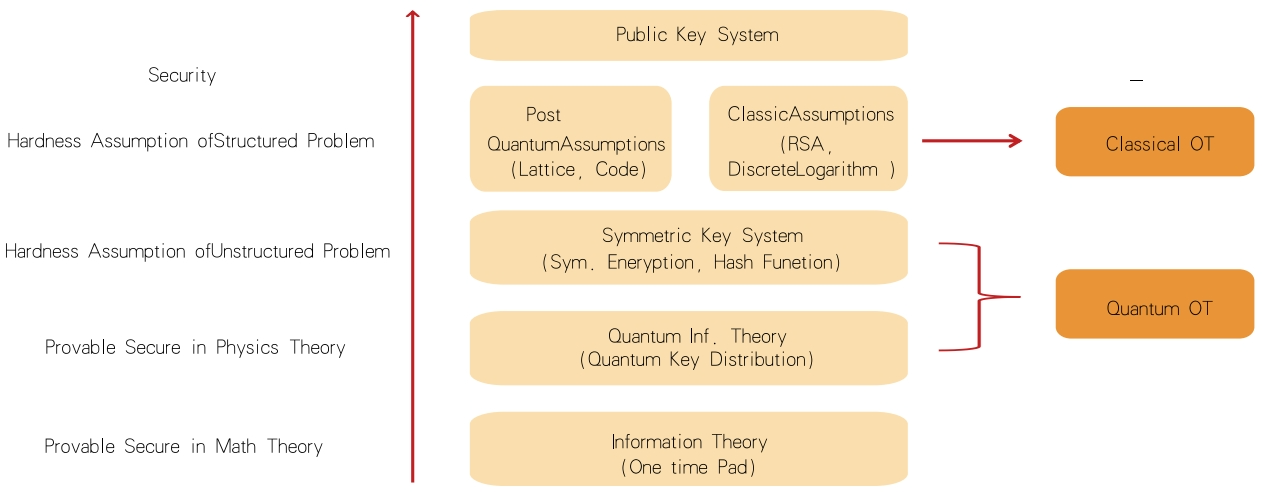
图4 不同密码系统假设对比

 

在安全性方面，相比已有的基于量子通信的QOT用不可见”的安全计算模式；秘密共享和同态秘密共享技术通过将数据分割计算，在提升数据安全性的同时，还大幅提高了计算效率。这一综合性计算方案具备强大的功能，能够支持各类复杂计算任务，确保在整个计算过程中数据隐私和安全万无一失。QOT在性能和安全性两方面的突破基于QKD的BB84协议，创新性地构造了量子不经意传输（QOT）协议。该协议具备多方面的优势。从抗量子攻击特性来看，密码技术是隐私计算安全的基石。融合量子信息技术的密码学假设结构中，不同的假设强度不同，相应的密码算法或协议可靠性也有所差异。经典的OT协议通常基于公钥密码实现，依赖传统密码学假设，在量子计算时代存在明显的安全隐患，容易受到量子攻击。而QOT协议，通过使用QKD和对称密钥加密构建。如图4所示，它所基于的密码学假设比经典OT更弱，甚至比后量子密码构建的OT协议（PQC—OT）还要弱。这是因为该协议仅需要量子安全的比特承诺方案，此方案依赖于单向置换或抗碰撞性哈希函数，这两者都属于无结构的对称数学问题，量子计算机难以破解，并且单向函数是量子领域中所需的最小假设。因此，从理论分析上，QOT协议具备更强的抗量子安全性。在安全性方面，相比已有的基于量子通信的QOT研究，该协议采用比特承诺方案，确保了在“存储—测量”攻击下协议的安全性。即使恶意的Bob试图通过量子存储延迟测量来获取Alice的全部信息，协议依然安全。此外，该方案采用成熟的BB84协议通信方式，与尚处于实验阶段的纠缠类协议相比，成码率更高。这不仅能破解比特承诺方案量子通信量消耗大的问题，还能提升QOT协议的性能。而且，借助BB84通信方式对物理层分光攻击（PNS）的诱骗态协议方案，可避免Bob利用分光攻击加“存储—测量”的手段骗取Alice的全部信息，全面保障了QOT协议的安全性。

 

在量子不经意传输组网方面，根据QOT协议的构造原理，底层借助BB84的QKD协议进行量子信道通信，上层应用则通过传统网络运行QOT经典协商协议来实现工程落地。但当前QOT通信双方的地理距离受限于量子通信设备的光纤成码距离，一般只有几十公里，仅适用于同城两节点之间的短距离单向安全多方计算场景，无法满足安全多方计算中远距离（跨域）多节点之间的双向不经意传输需求。因此，QOT的跨域远距离组网技术成为基于量子信息的安全多方计算迈向规模化应用的关键。

 

效能评估与应用验证

 

效率评估

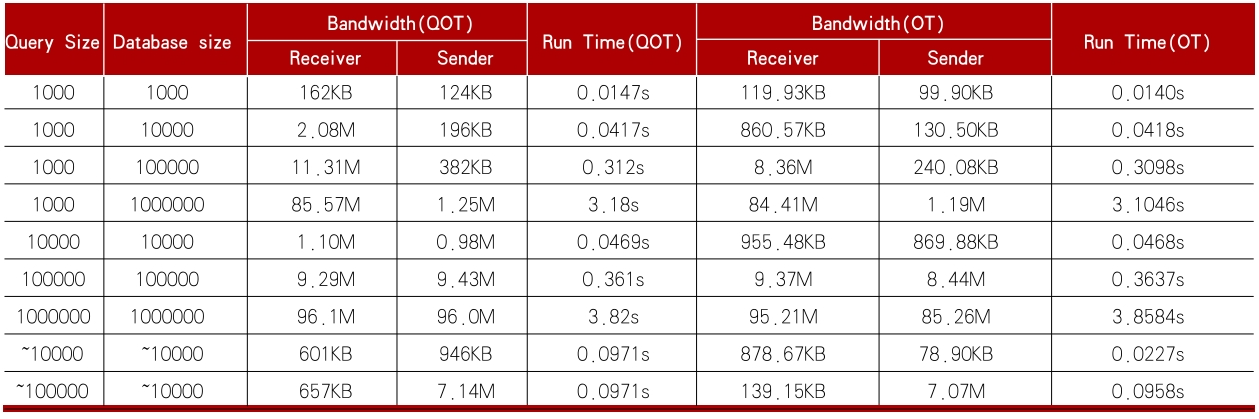
通过使用QOT替代传统OT，实现不经意伪随机函数协议，并在模拟数据和真实数据上进行了验证。如望未来，该领域的研究将主要集中在以下三个方向：首表1所示，在模拟数据验证中，随机生成了1k、10k、100k、1M量级的数据。实验结果表明，QOT协议在保证效率和正确性的同时，能够抵御潜在的量子攻击，可有效替代传统方法。此外，研究还提出了一种优化的同态秘密共享（OHSS）。

 

表1 QOT性能测试

        

 

通过改进算法设计和资源分配策略，OHSS在保证抗量子特性的同时，能够高效支持“矩阵-向量乘法”和“矩阵-矩阵乘法”，提升了复杂计算场景下的处理能力。

 

应用验证

2024年上半年，研究团队围绕反电信欺诈场景，开展基于量子不经意传输（QOT）的隐私计算协议技术验证。通过在同城金融机构数据中心搭建现网实验环境，采用生产数据进行抗量子隐私集合求交测试，成功验证QOT技术在隐私计算领域的可行性。同年下半年，研究团队进一步深化QOT组网方案验证，基于已建成的区域量子城域网，实现机构间量子不经意传输，并完成隐私集合求交与匿名查询协议开发，拓展了QOT技术的应用边界。基于前期研究成果，2025年研究聚焦于抗量子隐私计算体系在反洗钱非现场监管场景的理论研究与工程化应用探索。

 

未来方向与战略意义

 

量子安全隐私计算体系的构建，标志着密码学从“经典防御”迈向“量子—经典协同”的全新范式。展望未来，该领域的研究将主要集中在以下三个方向：首先，深入探索量子密码算法与隐私计算的深度融合，进一步挖掘量子技术在数据处理与分析中的巨大潜力，推动量子安全隐私计算的创新突破。其次，加速标准化进程，制定量子不经意传输（QOT）协议的互操作规范以及后量子密码迁移指南，以促进量子安全隐私计算技术的广泛应用和不同系统间的无缝互联互通。最后，构建开放生态，通过提供量子密码即服务（QPaaS）和隐私计算即服务（PCaaS），为企业和机构提供便捷、高效的量子安全服务，助力量子安全隐私计算的广泛应用。

 

（龙盈智达〔北京〕科技有限公司首席数据科学家王彦博对本文亦有贡献）

 

【参考文献】

[1]慢雾. 2024区块链安全与反洗钱年度报告[R/OL].（2025-01-03） . https://www. slowmist.com/report/2024-Blockchain-Security-and-AML-Annual-Report(CN) . pdf.

 

[2]北京金融信息化研究所.金融反欺诈与大数据风控研究报告（2023）[R/OL].（2024-01-23）.https://www.vzkoo.com/document/20240123a69beb39e24940e210077a1a.html.

 

[3]Susnjara S,Smalley I.What is quantum-safe cryptography?[R/OL].（2024-09-04） .https://www.ibm.com/think/topics/quantum-safe-cryptography

 

[4]SZhang,J Bai, K Tu, et al. OHSS:Optimizing Homomorphic Secret Sharing to Support Fast Matrix Multiplication, December 17-21, 2024[C] . 2024 IEEE 23rd International Conference on Trust ,Security and Privacy in Computing and Communications(TrustCom), Sanya : China, 2024.

 

[5]中国人民银行.金融数据安全数据安全分级指南：JR/T0197-2020[S],2020.

 

[6]Bos J,Ducas L,Kiltz E,et al.CRYSTALS-Kyber:A CCA-Secure Module-Lattice-Based KEM[C]//IEEE European Symposium on Security & Privacy. IEEE, 2018.DOI:10. 1109/EuroSP . 2018 . 00032.

 

[7]国家密码管理局.SM3密码杂凑算法：GM/T0004-2012[S],2012.

 

[8]国家密码管理局.SM4分组密码算法：GM/T0002-2012[S],2012.

 

[9]李子臣,张玉龙,杨亚涛.密文类型可修改的基于格代理重加密方案[J].计算机应用研究,2017,34(1):224-228.

 

[10]汤海婷,汪学明.一种基于格的属性多重加密方案[J].计算机工程,2018,44(2):193-196.

 

作者单位：成方金融科技有限公司，国科量子通信网络有限公司，

上海交通大学，其中涂锟系成方金融科技有限公司新技术实验室总经理，

黄安静系国科量子通信网络有限公司副总工程师

 

责任编辑：张志敏